Background
Session recommendation:
Aiming to predict the next item to be interacted with a user under a specific type of behavior, and modeling user dynamic interest.
Target behavior session recommendation:
Considers target behavior and auxiliary behavior sequences and explores for accurate prediction.

Challenges
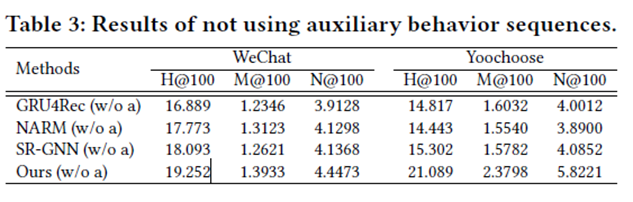
- Firstly, most existing methods focus on only using the same type of user behavior as input for the next item prediction, but ignore the potential of leveraging other type of behavior as auxiliary information.
- Secondly, item-to-item relations are modeled separately and locally, since both RNN based and GNN based recommendation models only utilize one behavior sequence each time.
Contribution
- We break the restriction of only using one type of behavior sequence in session-based recommendation and exploring another type of behavior as auxiliary information and construct the multirelational item graph for learning global item-to-item relations.
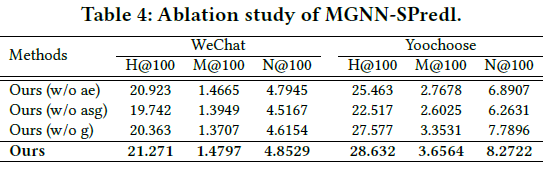
- we develop the novel graph model MGNN-SPred which learns global item-to-item relations through graph neural network and integrates representations of target and auxiliary of current sequences by the gating mechanism.
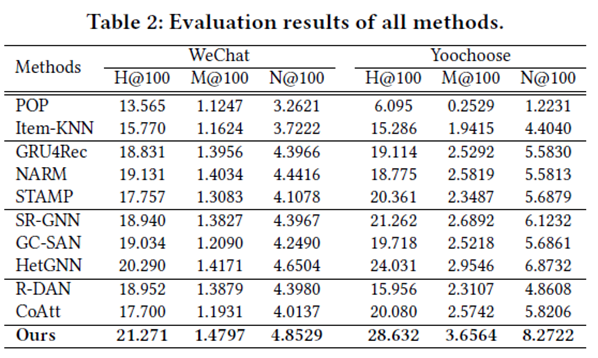
- We carry out extensive experiments and demonstrate MGNNSPred achieves the best performance among strong competitors.
Method
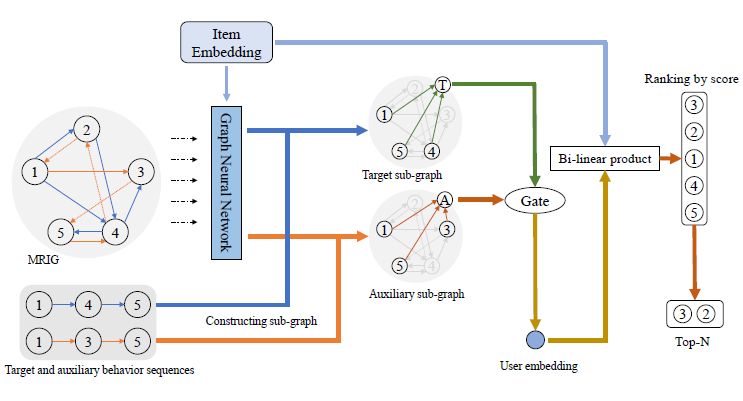
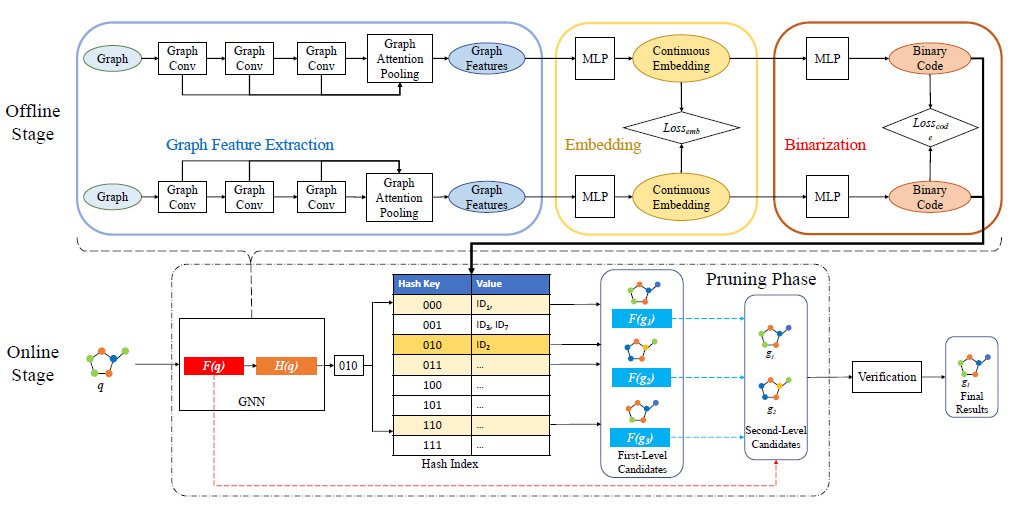
Problem Definition
• Session set: $S$
• Target behavior sequence: $P^s=[p1^s,⋯,p|P^s |^s]$
• Auxiliary behavior sequence: $Q^s=[q1^s,⋯,q(|Q^s |)^s]$
• Multi-Relational Item Graph: $G=(V,E)$, $V$ is the set of nodes in the
• graph containing all available items and $E$ is the edge sets involving
• Multiple types of directed edges. Each edge is a triple consisting of the head item, the tail item, and the type of this edge. Edge $(a, b, click) ∈ E$ means that a user clicked item $b$ after clicking item $a$.
Graph Construction
The algorithm browses all behavior sequences, collects all items in the sequences as the nodes of the graph, and constructs edges between two consequent items in the same sequence with their behavior types as the edge types.

Item Representation Learning
For each node $v∈V$, first convert them to a space $E∈\mathbb{R}^{|V|×d}$, and feed them with MRIG into GNN.
Each node in the graph has four types of neighboring node sets. According to the type and direction, we name the four sets as “target-forward”, “target-backward”, “auxiliary-forward”, and “auxiliary-backward”.
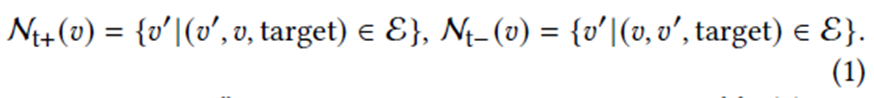
Same for the auxiliary set.
Item Representation Learning
First aggregate each group of neighbors by mean-pooling to obtain the representation of this group, defined as below:
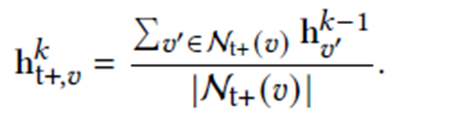
Then, we combine these four representations of different neighbor groups by sum-pooling:
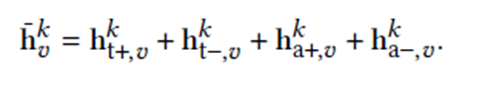
Finally, we update the representation of the center node 𝑣 by:
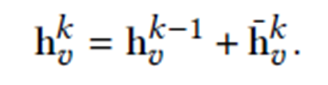
Sequence Representation Learning
Mean pooling the target behavior sequence $𝑃$ and auxiliary behavior sequence $𝑄$ as $p$ and $q$, respectively, which are given as:
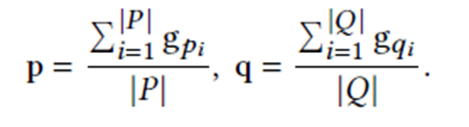
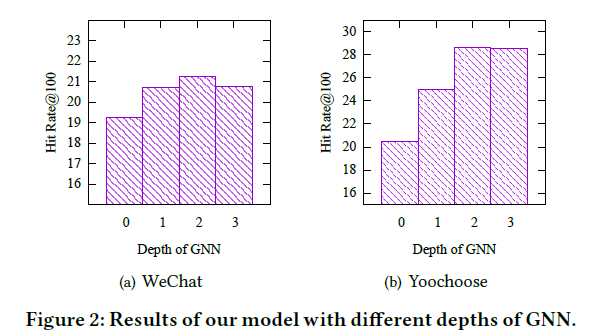
where $g_v=h_v^K$, and $K$ is the total iterations of the GNN.
A gate mechanism to calculate the relative importance weight $𝛼$
$o$ for the current session by the weighted summation of $p$ and $q$:
Model Prediction and Training
We further calculate the recommendation score $𝑠_𝑣$ of each item $v ∈V$ using the item embedding $e_v$ . A bi-linear matching scheme is employed by:
Over all items to get the probability distribution $\hat{y}$:
Loss function:
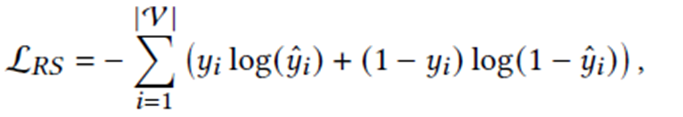
Experiment
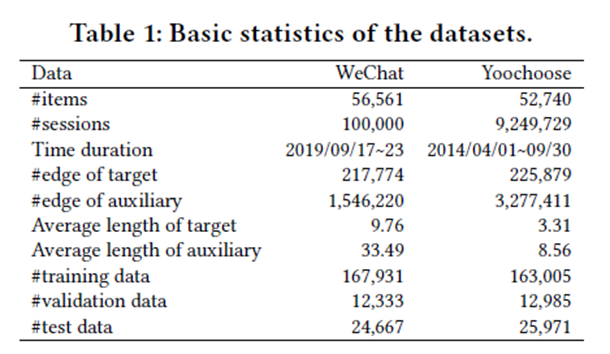
Datasets:
Baselines:

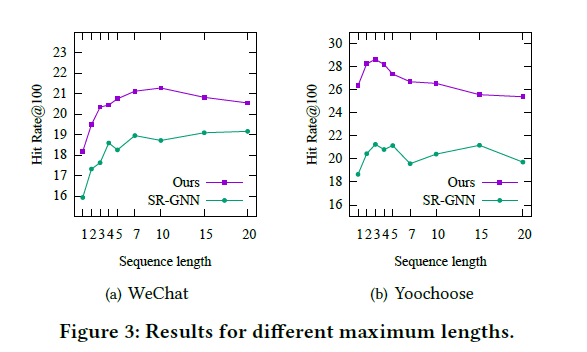
Results