Breaking the Limits of Message Passing Graph Neural Networks

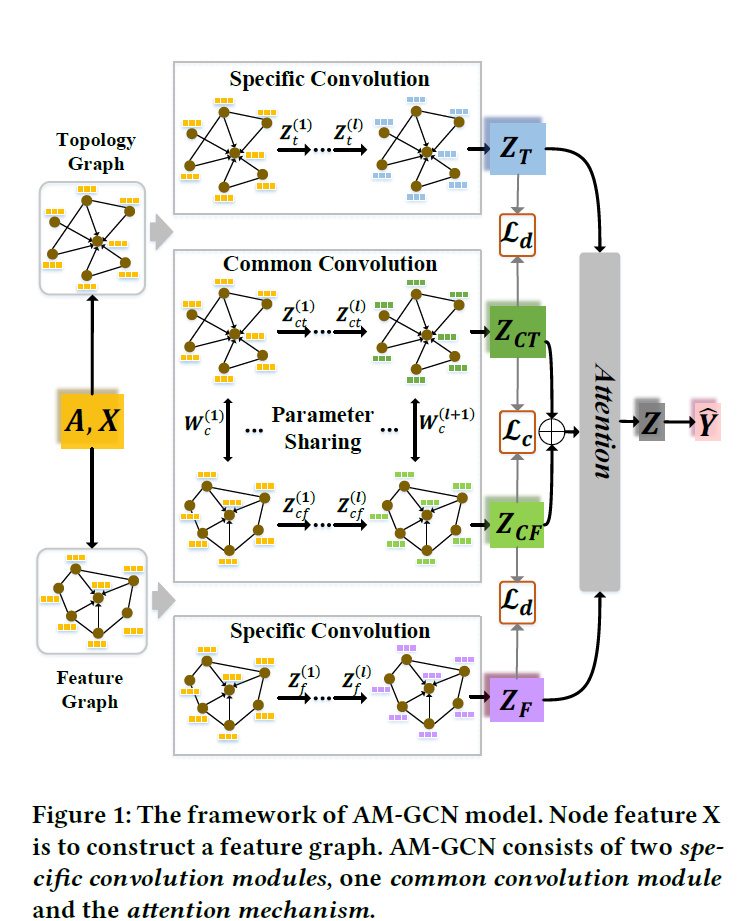
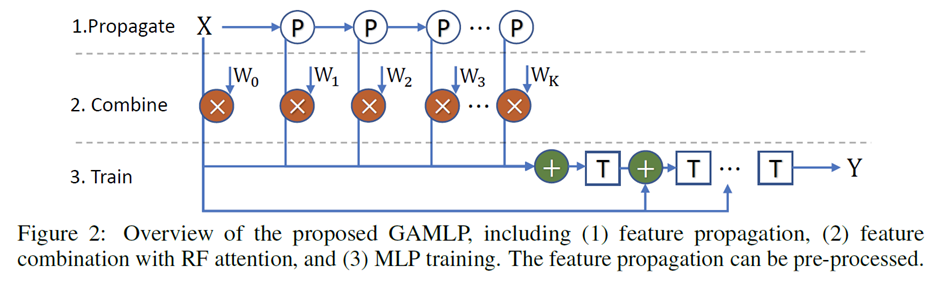
Motivation

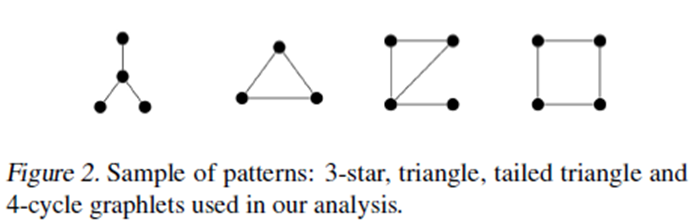
1. Existing GNNs’ expressive power is limited to 1-WL test, thus they cannot count some substructures likes: triangle, tailed triangle, and 4-cycle graphlets

1. Existing beyond 1-WL test GNNs is computational heavily $O(n^3)$ and memory hungry $O(n^2)$.

2. Some methods introduce some handcrafted features that cannot be extracted by GNN into the node attributes to increase the GNN’s expressive power: Distance encoding, identity GNN, and some Jure’s works.

3. Existing GNN focuses on the low pass frequency component.

Contribution

1. Give the explanation of what make GNN has certain expressive power.

2. Propose a graph convolution method (GNNML) that is more powerful than 1-WL test and reaches the 3-WL test.

3. GNNML has linear memory and computational complexities.

4. Enough spectral ability and local update process.

Road Map

GNN->WL test->Matrix Language-> GNNML

Weisfeiler-Lehman Test (WL-test)

1-WL test

Consider the 1-vertex.

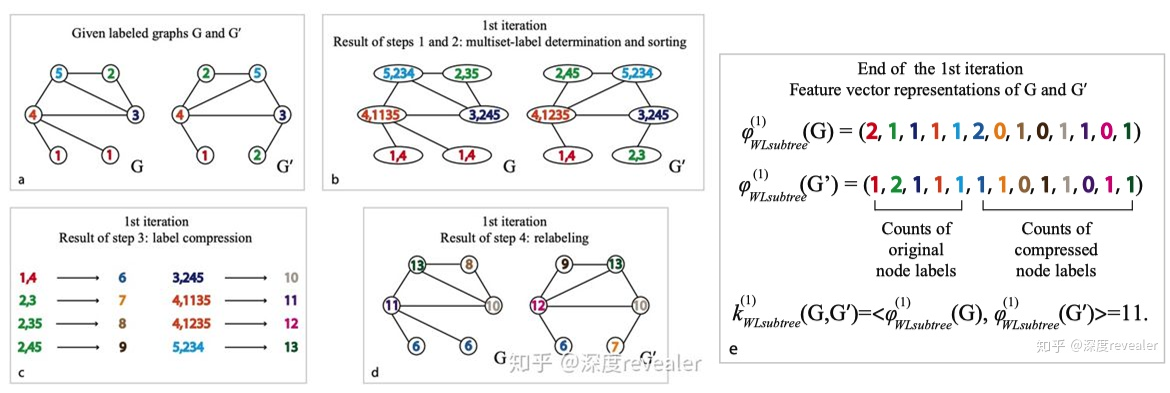
k-WL test

Consider k-vertex tuple.

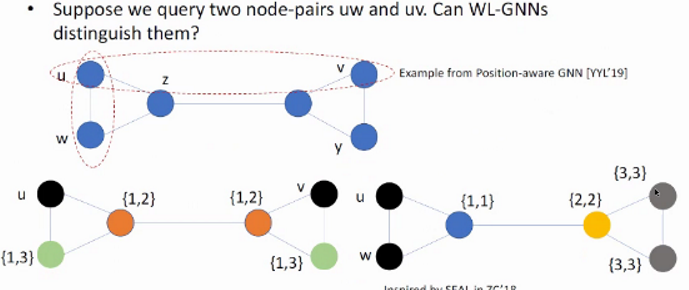
Examples of non-isomorphic graphs that cannot be distinguished by 1-WL but can be distinguished by 3-WL due to its capability of counting triangles.

Matrix Language and WL test

Matrix Language (MATLANG) includes different operations on matrices and makes some explicit connections between specific dictionaries of operations and the 1-WL and 3-WL tests

Definition 1: $ML(\mathcal{L})$ is a matrix language with operations set $\mathcal{L}={op_1,⋯,op_n }, op_i\in{⋅,+,⊤,diag, tr,1,⊙,×,f}$

Definition 2: $e(X)∈\mathbb{R}$ is a sentence in $ML(\mathcal{L})$ if it consists of any possible consecutive operations in $\mathcal{L}$, operating on a given matrix $X$ and resulting in a scalar value.

Example: $e(X)=\mathbf{1}^\top X^2\mathbf{1}$ is a sentence of $ML(\mathcal{L})$ with $\mathcal{L}={⋅,⊤,\mathbf{1}}$

Matrix operation can extract different features from the graph that can be used to differentiate the graph.

Remark 1: Two adjacency matrices are indistinguishable by the 1-WL test if and only if $e(A_G )=e(A_H)$ for all $e∈L_1$ with $L_1={⋅,⊤,1, diag}$.

Remark 2: $ML(L_2 )$ with $L_2={⋅,⊤,1,diag,tr}$ is more powerful than 1-WL test but less powerful than 3-WL test.

Remark 3: $ML(L_3 )$ with $L_3={⋅,⊤,1,diag,tr,⊙}$ is as powerful as 3-WL test.

Remark 4: Enriching operation set to $L^+=L∪{+,×,f}$, $L∈(L_1,L_2,L_3) $ cannot improve the expressive power.

How powerful are GNNs?

Theorem 1: Spatial GNNs such as GCN, GAT cannot go further than 1-WL test ($ML(L_1^+)$)

Theorem 2: Chebnet (Spectral GNN) is more powerful than the 1-WL test if the Laplacian maximum eigenvalues of the non-regular graphs to be compared are not the same.

Theorem 3: 3-star graphlets can be counted by sentences $L_1^+$

Theorem 4: Triangle and 4-cycle graphlets can be counted by sentences $L_2^+$

Theorem 5: Tailed triangle graphlets can be counted by sentences $L_3^+$

Generalization of Spectral and Spatial GNN

Spectral GNN

$$X=Udiag(Ω(λ)) U^⊤$$

Spatial GNN

$$X=AHW$$

Generalization GNN

$$H^{(l+1)} = \sigma(\sum_sC^{(s)}H^{(l)W^{(l,s)}})$$

where $C^((s))∈\mathbb{R}^{(n×n)}$ is the $s$-th convolution support that defines how the node features are propagated to the neighboring nodes (different aggregation methods)

GNN beyond 1-WL

As aforementioned, the K-WL test can be represented by some matrix operations. Thus, the GNN contains the certain operations can also have the express power of k-WL test.

The paper proposes two methods. The first one, called GNNML1 is shown to be as powerful as the 1-WL test. The second one, called GNNML3 exploits the theoretical results of to break the limits of 1-WL and reach 3-WL equivalence experimentally.

GNNML1

Proof: The GNNML1 can produce all possible vectors in $L_1={⋅,⊤,1,𝑑𝑖𝑎𝑔}$

GNNML3

To reach more powerful models than 1-WL, the graph convolution must support trace ($tr$) and multiplication ($⊙$) operation in $L_3$.

The trace (tr) and multiplication (⊙) operation often take effect in high power of adjacent matrix.

However, we cannot initially know which power of adjacency matrix is necessary for a given problem.

Thus paper designs a spectral convolution support that can be expressed as a linear combination of all powers of adjacency matrix.

With the any power of the adjacency matrix, the trace ($tr$) and multiplication ($⊙$) operation can be approximated by MLP (A trick ! MLP can approximate every function~)

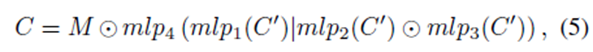
Where M can be seen as a mask (attention matrix) to select certain powers of the adjacency matrix.

The forward calculation of GNNML3 is :

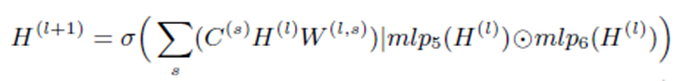
Where $C^s$ can be seen as a multi-heads attention of different graph structure components to provide different operations’ result vector that can be used to approximate 3-WL test.

Experiments

Q1: How many pairs of non-isomorphic simple graphs that are either 1-WL or 3-WL equivalent are not distinguished by the models?

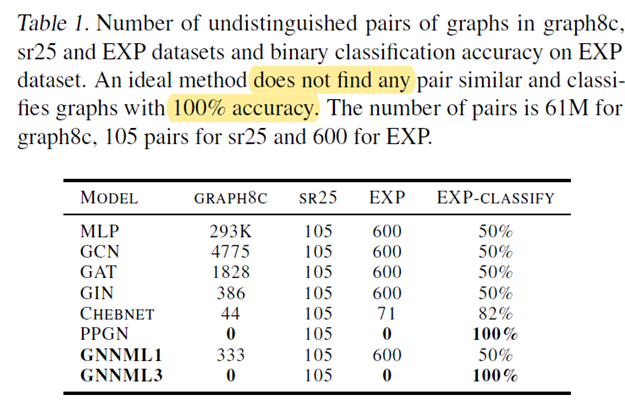
Q2: Can the models generalize the counting of some substructures in a given graph?

Q3: Can the models learn low-pass, high-pass and bandpass filtering effects?

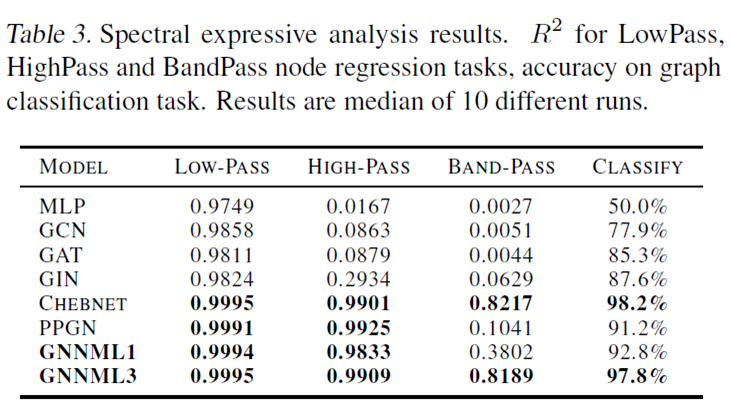
Q4: Can the models generalize downstream graph classification and regression tasks?

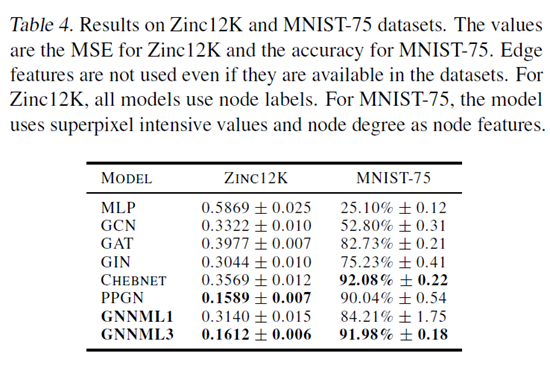
Conclusion

1. Theoretically give the explanation that to reach different express power (k-WL test) what operations GNN should have. It will help the successors find way to further improve the express power of GNN.

2. The multiple convolution supports used in GNNML3 is actually a multi-heads attention of different graph structure components to provide different operations’ result vector that can be used to approximate 3-WL test.

3. It cannot theoretically prove the GNNML3 is equal to 3-WL test, because its use the MLP to approximate the trace and multiplication operations.